
Qu'est-ce que la loi de Blondel ?
Certains théorèmes, équations et formules mathématiques sont bien connus du grand public (Pythagore, Thalès, Newton et Einstein par exemple). D’autres le sont beaucoup moins. C’est notamment le cas de la Loi de Blondel. Loi de qui ? Et pour quoi ? Pour le savoir, suivez sans plus attendre les explications de Bricozor qui vous présente aujourd’hui une formule toujours employée par les professionnels du secteur pour concevoir des escaliers aussi agréables que sûrs à utiliser.
Présentation de François Blondel et élaboration de sa loi
Beaucoup de formules tirent leur nom de leur inventeur. C’est le cas de la loi de Blondel. Cette personnalité du XVIIe siècle a posé les bases d’un principe toujours en vigueur quatre siècles plus tard. Une longévité qui mérite bien un petit rappel biographique.
François Blondel, mathématicien et architecte

Né dans l’Aisne à Ribemont en 1618, François Blondel étudie les langues étrangères et les mathématiques avant d’embrasser une brillante carrière dans la Marine, qu’il quitte ensuite pour entrer au service du secrétaire d’État Loménie de Brienne. Chargé de l’éducation de son fils, François Blondel parcourt l’Europe et se passionne pour l’architecture.
De 1657 à 1663, il effectue différentes missions diplomatiques pour Mazarin en Europe, en Turquie et en Russie, et met à profit ses déplacements pour étudier et dessiner de nombreux bâtiments et structures.

Nommé conseiller d’État en 1663 puis ingénieur du Roy pour la Marine en 1664, François Blondel supervise des travaux de fortification en Normandie. En 1669, il entre à l’Académie des Sciences puis se voit chargé de reconstruire plusieurs portes de Paris. En 1671, Louis XIV le nomme directeur et professeur de l’Académie royale d’architecture.
En 1675, il publie le fameux Cours d’architecture enseigné à l’Académie royale d’architecture, dans lequel il énonce le principe de sa loi qui passera à la postérité sous le nom de loi de Blondel. Il meurt à Paris en 1686 après avoir consacré ses dernières années à étudier sa discipline de prédilection.
Naissance de la formule de Blondel

Outre sa passion pour les édifices, l’intérêt de François Blondel s’est également porté sur de nombreuses particularités architecturales comme les escaliers, souvent irréguliers à l’époque et de fait dangereux, dont il a étudié la construction en vue de les améliorer.
Mathématicien de formation, Blondel s’est penché sur ce problème en élaborant puis calculant pour cela une profondeur de marche idéale basée sur une unité de longueur, le pas.
Objectif : offrir au pied une surface d’appui suffisamment grande pour lui assurer équilibre et stabilité entre chaque marche et créer un rythme de montée et de descente régulier. Une évidence pour nous aujourd’hui, mais loin d’être le cas au XVIIe siècle.
Utilisation de la formule de Blondel

Les escaliers renvoient de nos jours une image parfaite dans laquelle chaque élément (marches, rampes, poteaux et limons par exemple) semble naturellement s’emboîter pour un résultat final à la fois esthétique, confortable et sûr.
En réalité, un escalier demande du temps, de la réflexion, des prises de mesures, et la maîtrise d’indispensables formules de calcul, comme celle élaborée par Blondel.
Éléments de calcul de la formule de Blondel
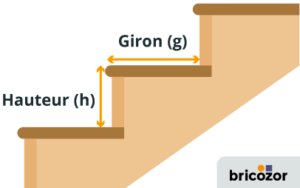
Pour effectuer le calcul tel qu’énoncé par Blondel, deux données doivent impérativement être connues et mesurées : le giron (g) et la hauteur de marche (h).
Pour rappel, le giron désigne la distance horizontale entre deux nez de marche tandis que la hauteur de marche désigne la distance, verticale cette fois, entre deux nez de marche. Blondel quant à lui fournit une longueur, celle du pas, comprise selon lui entre deux valeurs : 60 et 64 cm.
Formulation de la Loi de Blondel
La formule de Blondel est la suivante :
60 < g + 2h < 64
Pour la décrypter, rien de tel qu’un petit exercice pratique.
Prenez un mètre et approchez-vous d’un escalier. Mesurer le giron (g) et la hauteur de marche (h). Sinon, voici les valeurs suivantes, présentes sur des escaliers existants : g = 22 cm et h = 20 cm.
Le calcul s’effectue ainsi : 22 + (2 x 20) = 22 + 40 = 62 cm.
Cette valeur étant comprise entre 60 et 64 cm, l’escalier mesuré respecte bien la loi de Blondel en termes de confort de franchissement. C’est aussi simple que cela.
Au moment de son élaboration, toute la difficulté pour un menuisier va bien évidemment consister à définir en amont un giron et une hauteur de marche correspondant à cette loi.

De même, il est important de noter qu’un escalier qui répond à une loi de Blondel peut se révéler inconfortable à l’usage. La conception d’un escalier nécessite de tenir compte de nombreux autres paramètres, comme la hauteur de la trémie par exemple.
L’expertise du professionnel se situe précisément dans cette capacité à tenir compte de tous pour un résultat final réussi.
Bien que très ancienne, la loi de Blondel fonctionne toujours aussi bien.

En bois, en pierre ou bien encore en métal, peu importe le matériau. Ce qui compte, c’est le confort et la sécurité attachés à son utilisation. Un escalier bien élaboré se gravit et se descend sans réfléchir, de manière automatique. Les pieds viennent se poser spontanément sur les degrés dans un enchaînement ininterrompu, de la base vers le sommet (ou inversement).
En attachant de l’importance à l’espace occupé par le pas sur une marche, François Blondel peut donner l’impression de s’être consacré à une tâche bien futile. Or, grâce à lui et à sa formule, nous pouvons, plus de trois cent ans après sa disparition, nous déplacer dans un escalier sans l’ombre d’une hésitation.
" Les détails font la perfection, et la perfection n'est pas un détail "
En voici une belle illustration.



